Integrated Photonic Gyroscopes

I.   Introduction

A gyroscope is an angular motion detection device [1]. In the inertial navigation system [2]–[5], the gyroscope accurately can measure the angular velocity of the carrier in the inertial reference system, and then further calculates the speed, angle, and position information [6]. Therefore, navigation system with the gyroscope are applied to aircraft, warships, submarines, satellites, space launchers and other fields [7]–[10].

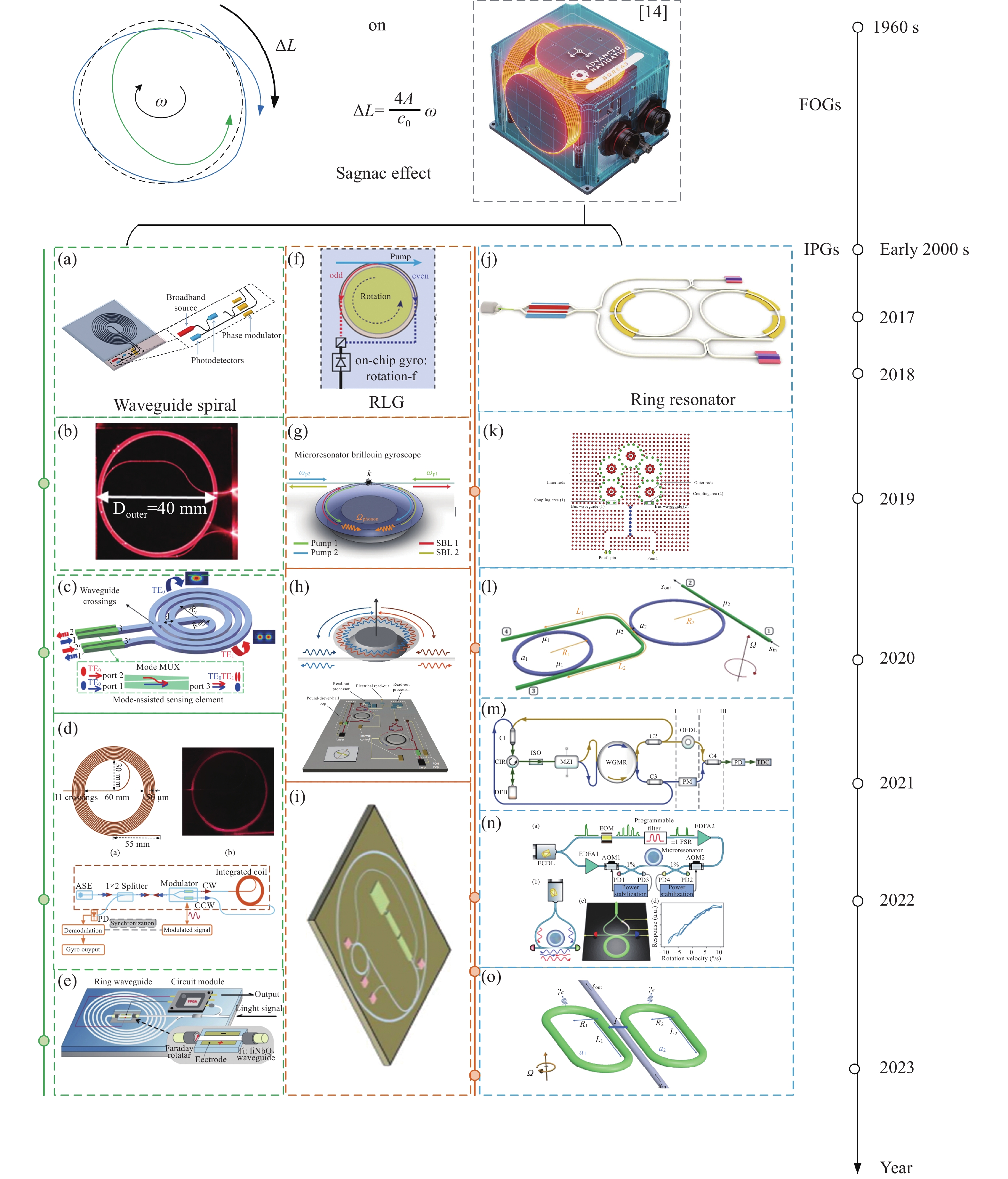
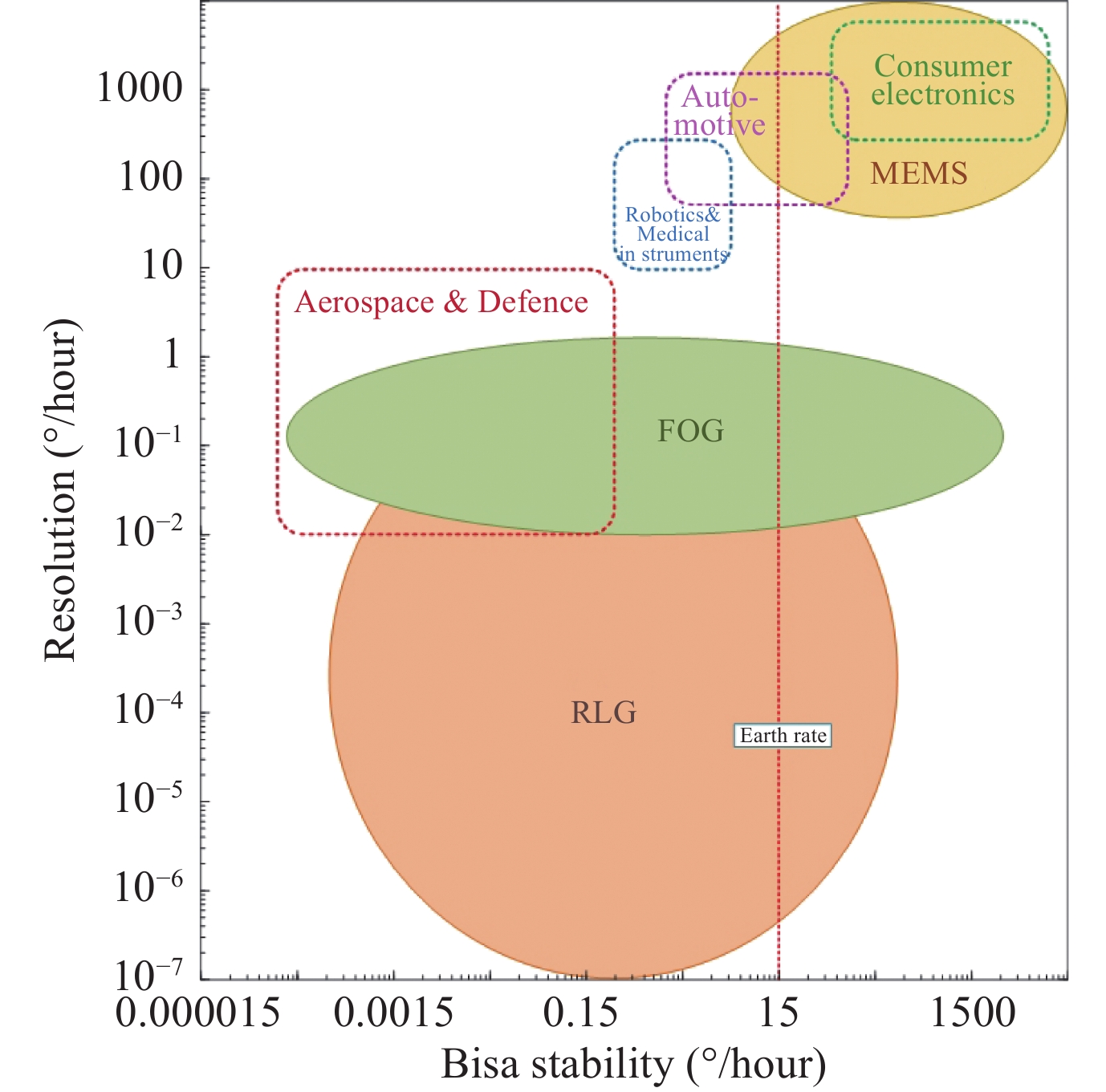
According to different working principles, gyroscopes can be divided into mechanical gyroscopes, microelectronic gyroscopes and optical gyroscopes. The mechanical gyroscope is a mechanical device that measures angular velocity based on mechanical properties [11]. Microelectronic gyroscope is composed of vibrating mechanical parts and it can use Coriolis force to measure angular velocity [12]–[15]. They have met the market request and offered high performance for industrial and other fields. Figure 1 show applications and requirements for different gyroscope technologies. However, they suffer from several drawbacks, including high power consumption, large size, mechanical wear, tear, shock, and vibration. Compared with mechanical and microelectronic gyroscopes, Optical gyroscopes [16]–[18] have the advantages of high accuracy, long service life, no moving parts and good impact resistance [19], [20]. Optical gyroscope is composed of discrete devices and their manufacturing costs and power consumption are high, which doesn't meet the needs of ordinary consumers.

Figure  1.  Applications and requirements for different gyroscope technologies [39]–[43].

DownLoad: Full-Size Img PowerPoint

IPGs utilize the interference of light waves in a waveguide to measure angular rotation, which allows for high sensitivity, compactness, and low power consumption. Compared with mechanical gyroscopes and MEMS gyroscopes, IPGs has a longer life, higher accuracy, and more stability. Therefore IPGs have emerged as a promissing alternative to traditional mechanical gyroscopes [21]. The integration of photonic components such as waveguides, modulators, and detectors onto a single chip has enabled the development of small, low-power IPGs with high sensitivity and bandwidth [22]–[24].

With the development of IPGs, some IPGs were proposed based on different material platform such as $\mathrm{LiNbO_3}$ [25], [26], Polymer Materials [27], [28], InP [29], [30], $\mathrm{SiO_2}$ [31], [32], $\mathrm{Si_3N_4}$ [33], [34], $\mathrm{CaF_2}$ [35], [36]and Silicon on insulator(SOI) [37], [38]. In recent years, significant research and development in IPG technology have been conducted focusing on improving their stability, accuracy, and resolution. Different types of IPGs have been developed, including waveguide spiral-based, RLG IPGs, and passive ring resonator IPGs, each with advantages and disadvantages. Waveguide spiral-based IPGs use on-chip waveguide spiral to detect rotation, while RLG IPGs rely on the beams of light transmitted clockwise and counter clockwise by the same light interference. Passive ring resonator IPGs utilize the resonance of light in a ring-shaped cavity to measure rotation.

In addition to improving the stability, accuracy, and resolution of IPGs, efforts have been made to integrate them with other devices to create compact and low-power navigation systems.

This review aims to provide an overview of recent advances in IPG technology and research. We discuss efforts to improve the stability, accuracy, and resolution of IPGs, such as the use of narrow-band laser diodes. Furthermore, we review the calculation of key performance factors for IPGs and their interrelationships, including resolution, drifting, stability, noise cancellation, and more. We also highlight the challenges that remain to be addressed, such as improving long-term stability and addressing sensitivity to shock and vibration. Finally, we discuss possible future directions for IPG research, such as the use of new materials and geometries, and the integration of IPGs with other emerging technologies.

II.   Theory and Operating Principle

The gyroscope equation is an equation that describes the behavior of a spinning object in an angular velocity. It can be written as:

where $\Omega$ is the angular rotation rate, n is the refractive index of the fiber, L is the length of the fiber, $\lambda$ is the wavelength of light used, and $\Delta$ND is the difference in the number of refractive modes in the two directions of the fiber.

1   Waveguide spiral-based (sagnac-laue effect)

The equation for the Sagnac-Laue effect can be written as:

Where $\Delta\Phi$ is the phase shift, $A$ is the area enclosed by the path of the light, $\lambda$ is the wavelength of the light, $c$ is the speed of light, $n$ is the refractive index of the crystal, $d$ is the thickness of the crystal, and $\theta$ is the angle of incidence of the light on the crystal.

2   RLG

The ring laser gyroscope is based on the Sagnac effect. Two laser beams propagate in opposite directions in a closed ring cavity, and when the ring cavity rotates, the resonance frequency of the two laser beams will produce a blue shift and a red shift respectively. The shift results in a frequency difference, which is proportional to the rotation rate $\Omega$, and can be expressed as

where $A$ is the area of the ring cavity; $\lambda_{m}= \frac{c}{f_{m}}$ is the wavelength at rest; L is the perimeter of the ring shaped cavity.

3   Ring resonator

In the absence of IPGs rotation the ring cavity eigenfrequencies are equal and given by the expression

where $c$ is the velocity of light propagation in vacuum; $n$ is the refractive index of the optical material; $L$ is the perimeter of the ring shaped cavity; and $m$ is a positive integer. When the IPGs rotate in the plane with an angular velocity of ${\Omega}$. The eigenfrequencies are split due to the Sagnac effect, and $f_{mccw}$ and $f_{mcw}$ are eigenfrequencies of the cavity when the light propagates along the ring cavity in counterclockwise and clockwise directions respectively. The difference of eigenfrequencies is determined by the expression

Where A is the area of the ring cavity and $\lambda_{m}= \frac{c}{f_{m}}$ is the wavelength at rest.

III.   Performance Factor

In testing and evaluating integrated photonic gyroscopes (IPGs), certain performance factors are particularly critical. The importance of each factor can vary depending on the specific application and operational environment of the IPG. Here are some of the most important factors:

Resolution: This refers to the smallest angular change that the gyroscope can detect. High resolution is crucial for applications requiring precise angular measurements.

Bias Drift (Zero-rate Bias Stability): Bias drift indicates the change in the gyroscope’s output when it is stationary. It is essential for maintaining accuracy over time, especially in navigation systems where cumulative errors can significantly impact performance.

Angle Random Walk (ARW): ARW is a measure of sensor noise and is important in determining how quickly the error accumulates over time. Lower ARW values are desirable for precision applications.

Scale Factor Stability: This refers to the consistency of the gyroscope’s output relative to the actual rotation rate. Stability in the scale factor ensures that the gyroscope’s sensitivity remains constant over time and under varying conditions.

Bandwidth: The bandwidth of the gyroscope defines the range of frequencies over which the device can accurately measure rotation rates. Higher bandwidth allows for the accurate detection of rapid movements.

Temperature, Shock, and Vibration Sensitivity: Gyroscopes are often used in environments with varying temperatures and mechanical disturbances. Therefore, resistance to temperature fluctuations, shock, and vibrations is crucial for reliable operation.

Noise Cancellation and System Calibration: Effective noise cancellation techniques and accurate system calibration are essential for minimizing errors and improving the overall accuracy of the gyroscope.

Repeatability: This is the ability of the gyroscope to produce consistent readings under the same conditions. High repeatability is critical for applications where the gyroscope is used for precision measurements.

Bias Offset Error: This is the difference between the gyroscope’s output and the true value when the rate of rotation is zero. Minimizing this error is important for accuracy, particularly in inertial navigation systems.

The performance factors of gyroscopes are interdependent and complex. For example, improving temperature stability can enhance bias drift and scale factor stability, while reducing mechanical sensitivity (shock and vibration) improves both bias drift and ARW. Enhancements in noise cancellation techniques directly impact ARW and overall resolution.

The prioritization of these factors depends on the application. In aerospace, bias drift, ARW, and temperature stability are typically prioritized, while consumer electronics focus on size, cost, and power consumption. For navigation systems, long-term stability (bias drift and scale factor stability) and ARW are crucial. ARW measures the random fluctuations when a gyroscope is stationary and is usually expressed in degrees per square root hour $({^\circ}/{\sqrt{hr}})$ or radians per square root hour $(rad/\sqrt{hr})$. White noise power density refers to the noise intensity across different frequencies, expressed in degrees squared per hour or radians squared per hour. ARW is the square root of the integral of white noise power density over the frequency range, given by:

where $S(f)$ is the white noise power density, and $f_{1}$ and $f_{2}$ define the frequency band. This relationship is critical for designing and evaluating gyroscopes, especially in inertial navigation systems where low ARW minimizes long-term navigation errors. Understanding the white noise characteristics helps predict gyroscope performance in various scenarios. While the relationship between ARW and white noise power density is fundamental, it is usually discussed in more specialized literature, such as technical papers and textbooks on inertial navigation and sensor technology.

IV.   Different Types of Optical Gyroscope

1   Waveguide spiral-based

The sensitivity of the IPGs depends on the length of the fiber coil and is a major limitation to its size. The optical waveguide is placed in a Archimedean spiral shape in order to increase sensitivity and reduce the footprint. In addition, by spacing the waveguide crossings a coherence length away, the reflected light only adds in intensity and not phase. Figure 2(a) show that the waveguide spiral IPG was proposed at the hybrid silicon platform and it achieved an angle random walk (ARW) of 8.52°/$\sqrt{h}$, bias drift of 58.7°/h and resolution of 19°/hr/$\sqrt{H{\textit{z}}}$ [44]. In 2017, Taran Huffman’s team designed a waveguide spiral IPG. They measured a crossing loss of 0.0156dB/crossing in close agreement to simulations. This waveguide spiral IPG could reach an ARW of 69°/hr/$\sqrt{H{\textit{z}}}$ and the waveguide loss was near 0.58 dB/m [45].

Figure  2.  Timeline of integrated photonic gyroscope. (a) A integrated hybrid silicon waveguide optical gyroscope [44] (b) A waveguide spiral IPG [45]. (c) A mode-assisted on-chip silicon on insulator IPG [46]. (d) A interferometric optical gyro based on an integrated silica waveguide coil [47]. (e) A new ultra-short coil fiber optical gyroscope [48]. (f) A RLG based on a high-Q micro-ring resonator with 18mm [49]. (g) A RLG working near an exceptional point [50]. (h) A RLG integrated on a silicon chip for the purpose of measuring the Earth’s rotation rate [51]. (i) A kind of ring-laser IPG using Brillouin lasing in chip-scale [52]. (j) A ring-resonator gyroscope based on reciprocal sensitivity enhancement [53]. (k) A passive phase-sensitive integrated optical gyroscope based on photonic crystal ring resonator [54]. (l) An anti-parity-time symmetric optical gyroscope [55]. (m) A high-sensitivity RMOG based on a self-injection locking technique [56]. (n) A proof-of principle nonlinear enhanced micro-resonator gyroscope [57]. (o) A resonator-bus-resonator anti-parity-time-symmetric integrated optical gyroscope designed on InP platform for the first time [58]. Adapted From [44]–[58].

DownLoad: Full-Size Img PowerPoint

Afterwards, a mode-designed on-chip silicon on insulator(SOI) IPG was designed by using two different spatial modes counter propagating in the waveguide sensing coil. The counter-propagating spatial modes induce a fixed phase difference and IPG can achieve detect angular velocity sensitively. In addition, this IPG avoided phase modulator and circulator, thus significantly reduced complexity [46]. SiO₂ has been subject to intense research as an optical waveguide and then a interferomeric optical gyro based on an integrated silica waveguide coil was proposed which achieved that the bias drift was 7.32°/h and the ARW was 1.26°/$\sqrt{h}$ [47].

In a subsequent study, a team theoretically and experimentally proposed and analyzed a new ultra-short coil fiber optic gyroscope structure which fundamentally overcomes the shortcomings of traditional interferometric fiber optical gyroscope that are limited by time and eigenfrequency [48]. This approach lead to a new direction for the research on waveguide spiral IPGs.

2   RLG

The RLG uses the Sagnac effect to measure angular velocity. Its working principle involves emitting laser light into a closed ring cavity, where the light beams propagate in both clockwise and counter-clockwise directions. As the system rotates, the propagation times of the two beams are altered due to the Sagnac effect, resulting in a phase difference. By measuring this phase difference, the angular velocity of the rotation can be calculated. The phase difference is related to the path length of the light beams, the rotational speed, and the wavelength of the laser, making the RLG highly precise and stable. In 2017, Vahala’s team demonstrated a RLG based on a high-Q micro-ring resonator with 18mm which could utilize a single pump to trigger Brillouin lasing in a cascaded fashion to measure the frequency shift caused by Sagnac effect. This IPG could achieve a sensitivity of 15°/h/$\sqrt{H{\textit{z}}}$ [49]. Two years latter, this team proposed a RLG whose response to rotations was enhanced with working near an exceptional point where multiple eigenstates coalesce. They achieved precise control of the counter-propagating laser modes by matching the Brillouin gain with the resonator dispersion phase, and ultimately successfully observed a fourfold increase in the sagnac scaling factor [50]. Afterwards, they shew a RLG integrated on a silicon chip for the purpose of measuring the Earth’s rotation rate sensitively, and this RLG achieved an angle random walk noise of 0.068°/$\sqrt{H{\textit{z}}}$ and a bias drift 3.6°/h [51]. In 2020, Honeywell’s team proposed a kind of ring-laser IPG by using Brillouin lasing in chip-scale ${\mathrm{SiO}}_2$/${\mathrm{Si}}_3{\mathrm{N}}_4$. This RLG achieved 0.06 dB/m and could limit higher SBS orders and scattering loss of the light in the resonator [52].

3   Ring resonator

Ring resonator IPGs utilize a micro-ring resonator and the Sagnac effect to measure rotation. Light from a laser source is divided by a optical coupler into two waves, whose frequencies are controlled by two phase modulators. As the gyroscope spins, the optical paths traveling in two opposite directions differ, resulting in a resonant frequency difference of counter-propagating light due to the Sagnac effect. By detecting the resonant frequency difference, the rotation and the velocity can be calculated and obtained. Compared with waveguide spiral IPGs and RLG IPGs, IPGs with ring resonator usually have smaller footprint and lower power consumption, and then this type is more conductive to integrate.

In 2018, Parham P.Khial’s team utilized reciprocal sensitivity enhancement to design and implement a ring-resonator-gyroscope. This IPG could reach the bias of 1 r.p.m and an ARW of 650°/$\sqrt{h}$ [53]. In addition, some researchers also proposed a high-sensitivity RLG based on a self-injection locking technique by enhancing reciprocity and measuring beat frequency. This RLG can effectively measure angular velocity and increase sensitivity, and it has been demonstrated that the theoretical sensitivity of the RLG can reach $10^{-4}$ deg/h at a modulation frequency of 6 KHz [56].

In a subsequent study, researchers proposed the passive phase-sensitive integrated optical gyroscope (IOG) based on photonic crystal ring resonator (PCRR). The IOG was composed of two bus waveguides and five ring resonators. The ring resonators with different radii and refractive indices were used to improve the coupling efficiency. The angular velocity was calculated by calculating the transmission efficiency of the port [54].

A parity-time (PT)-symmetric gyroscope and an anti-parity-time (APT)-symmetric optical gyroscope are both designed based on the concept of parity-time symmetry. The PT-symmetric gyroscope exploits the property that physical systems remain invariant under simultaneous spatial inversion and time reversal, while the APT-symmetric optical gyroscope operates by leveraging the reverse parity-time symmetry within an optical system. The former may find applications in inertial navigation and precision measurement, whereas the latter could potentially be utilized in aerospace technology and precision navigation fields.

In 2019, Martino De Carlo et al. proposed the idea and design of an anti-parity-time (APT)-symmetric optical gyroscope that exhibits resonance splitting independent of device size. In contrast to the previously proposed parity-time (PT)-symmetric gyroscope, the solution demonstrates a true frequency split that can be measured directly at the output power spectrum. In addition, it can be kept at its exceptional point more accurately than the PT-symmetric counterpart [55]. Three years later, this team designed a novel anti-parity-time-symmetric IPG whose structure is resonator-bus-resonator on InP platform for the first time. Compared with other anti-PT symmetric gyroscope, this gyroscope only utilizes one auxiliary waveguide(central bus) to achieve better robustness [58]. There is a key features in ultrahigh-Q micro-ring resonator that they exhibit strong Kerr nonlinearity at low and moderate input power [34], [59], [60]. What’s more, Kerr interaction between counterpropagating light waves in micro-ring resonators can induce spontaneous symmetry breaking [61]–[63]. However, this symmetry breaking can enhances the response of the micro-ring resonator to rotation and result in critical slowing down [64], [65]. Based on this principle, researchers proposed a proof-of principle nonlinear enhanced micro-resonator gyroscope, which operates at the critical point of kerr-induced symmetry breaking between counter-propagating light in a bidirectionally pumped ring resonator, achieving a sensitivity of 2 deg/s [57].

From the data in Table 1, it is clear that there are significant performance differences among the three types of IPGs, specifically between waveguide spiral, ring laser, and passive ring resonator gyroscopes. Waveguide spiral IPGs generally show lower bias stability and much higher ARW compared to ring laser and passive ring resonator IPGs, making them less suitable for applications requiring high precision and long-term stability.

Table  1.  Performance metrics comparison of different integrated photonic gyroscopes.

Methods	Platform	Bandwidth	Bias Drift${}^\circ/h$	ARW ${}^\circ/\sqrt{h}$	Resolution	Footprint ${m^2}$
Waveguide spiral IPG[44]	$\mathrm{Si_3N_4}$	293 nm	58.7	8.52	19${}^\circ/h/\sqrt{H{\textit{z}}}$	$1.257\times{10^{-3}}$
Waveguide spiral IPG[45]	$\mathrm{Si_3N_4}$			1680		$2.1\times{10^{-3}}$
Waveguide spiral IPG[46]	$\mathrm{SOI}$	10 Hz				$3.85\times{10^{-3}}$
Waveguide spiral IPG[47]	$\mathrm{SiO_2}$	300 MHz		1.26		$1.21\times{10^{-2}}$
Waveguide spiral IPG[48]	$\mathrm{LiNbO_3}$					$4\times{10^{-4}}$
Ring laser IPG[49]	$\mathrm{SiO_2}$	>1 kHz			15${}^\circ/h/\sqrt{H{\textit{z}}}$	Diameter=18 mm
Ring laser IPG[50]	$\mathrm{SiO_2}$					Diameter=36 mm
Ring laser IPG[51]	$\mathrm{SiO_2}$		3.6	0.068		Diameter=36 mm
Ring laser IPG[52]	$\mathrm{SiO_2/Si_3N_4}$			<0.01
Passive ring resonator IPG[53]	$\mathrm{Si}$	several kHz	2160	650		$2\times{10^{-6}}$
Passive ring resonator IPG[54]	$\mathrm{Si}$	0.35 nm				$2.79\times{10^{-10}}$
Passive ring resonator IPG[55]	$\mathrm{}$					$3.2\times{10^{-9}}$
Passive ring resonator IPG[56]	$\mathrm{Si}$		$6\times{10^{-4}}$		$\times{10^{-4}}{}^\circ/h$	$3.3\times{10^{-4}}$
Passive ring resonator IPG[57]	$\mathrm{SiO_2}$				2°/s	Diameter=2.8 mm
Passive ring resonator IPG[58]	$\mathrm{InP}$					$2\times{10^{-6}}$

 | Show Table

DownLoad: CSV

For example, the bias stability of waveguide spiral IPGs ranges from $7.32 {}^\circ/h$ to $58.7{}^\circ/h$, while the bias stability of passive ring resonator IPGs can reach up to $2160 {}^\circ/h$, demonstrating a substantial performance gap. Similarly, in terms of ARW, waveguide spiral IPGs can have values as high as $1680 {}^\circ/\sqrt{h}$, while passive ring resonators achieve significantly lower values, down to $0.0006 {}^\circ/\sqrt{h}$. The ring laser gyroscopes also outperform waveguide spiral IPGs, with their bias stability as low as $3.6 {}^\circ/h$ and ARW reaching $0.01 {}^\circ/\sqrt{h}$ in the best case.

The resolution of the different types of gyroscopes also shows disparities, with passive ring resonator IPGs generally offering better performance, which is critical for high-precision applications. Furthermore, the footprint of waveguide spiral IPGs is larger, which impacts their potential for miniaturization. The smallest footprint of waveguide spiral IPGs is $4\times10^{-4}\; {\mathrm{m}}^{2}$, which is significantly larger than the $2\times10^{-6} \; {\mathrm{m}}^{2}$ footprint of the passive ring resonators.

Given these performance gaps, further discussion is needed on the trade-offs between bias stability, ARW, resolution, and size for different application needs. Waveguide spiral IPGs may be less suitable for high-precision navigation systems where long-term stability is crucial, while passive ring resonators are more ideal for such applications. However, the larger size and higher ARW of waveguide spiral IPGs may be acceptable in less demanding environments or where cost and integration are prioritized.

In recent years, IPGs have found their way into several cutting-edge applications that require high-performance inertial sensing. Aerospace and space exploration are key areas where passive ring resonator and ring laser gyroscopes are being deployed. These gyroscopes offer high bias stability and low ARW, crucial for long-duration missions in satellites, spacecraft, and space telescopes where precise orientation is critical. The European Space Agency (ESA), for instance, has integrated ring laser gyroscopes into spacecraft for precise attitude control.

Additionally, in the rapidly evolving field of autonomous vehicles, including both land-based and aerial drones, high-precision gyroscopes are essential for accurate navigation. Passive ring resonator gyroscopes, with their lower ARW and smaller footprint, are being explored for integration into LiDAR systems for real-time orientation correction and stability enhancement. These gyroscopes are also being employed in robotics to achieve high-precision inertial navigation in environments with minimal GPS access, such as indoor spaces or subterranean exploration.

Emerging technological trends are also advancing gyroscope performance. One such breakthrough is quantum-enhanced gyroscopes [66], which utilize quantum entanglement and squeezed states of light to minimize noise and improve measurement precision. These techniques are still in early development but show promise in exceeding classical gyroscope performance limits, especially in terms of reducing ARW and bias drift. Quantum-enhanced gyroscopes are expected to find applications in military and aerospace sectors, where ultra-precise orientation and stability are paramount.

Moreover, advancements in silicon photonics and photonics-on-chip technologies are paving the way for more compact, low-power, and cost-effective gyroscopes. Researchers are exploring photonic crystal structures and nonlinear optics to reduce optical losses, increase sensitivity, and improve thermal stability. These advances will enable gyroscopes to be integrated into smaller platforms like wearable devices and mobile phones, expanding the range of applications into the consumer electronics space.

Another promising technology is lithium niobate on insulator (LNOI), which offers superior optical confinement and allows for the development of more compact and efficient gyroscope designs. These advancements in materials could significantly reduce the footprint of gyroscopes, making them more feasible for mass deployment in sectors like automotive, medical devices, and precision agriculture.

As integrated photonic gyroscopes continue to evolve, there is a clear trajectory toward improving size, weight, power, and cost (SWaP) factors, which will broaden their applicability in both high-end and consumer markets.

V.   Disscussion

As we look ahead to the future of IPGs, a wave of exciting advancements and possibilities is on the horizon. These developments are poised to be driven by innovative strides in materials science, nanofabrication technologies, and integrated optics. The relentless pursuit of precision and miniaturization in nano-scale fabrication techniques is set to redefine the boundaries of IPGs, making them more compact yet incredibly precise. This evolution will open doors for IPGs to integrate into a diverse array of applications, from consumer electronics to autonomous vehicles, and even space exploration. Advancements in broadband light sources and state-of-the-art waveguide materials are anticipated to significantly elevate IPG performance. Such improvements promise enhanced noise reduction, heightened sensitivity, and bolstered stability against environmental factors, such as temperature shifts and mechanical vibrations. Furthermore, the prospect of integrating IPGs on chips with other photonic components, including lasers, modulators, and detectors, heralds the dawn of sophisticated, multi-functional photonic devices. This integration could revolutionize capabilities in communications, sensing, and imaging. Perhaps one of the most exhilarating frontiers is the convergence of quantum photonic technologies with IPGs.This quantum-enhanced IPG is expected to further improve sensitivity and accuracy. In the realm of autonomous technologies and the Internet of Things (IoT), IPGs are expected to be instrumental in providing precise navigation and orientation information, essential for the seamless operation of autonomous cars, drones, and various IoT devices. Moreover, the miniaturization of IPGs has the potential to make significant inroads in the biomedical field, particularly in applications demanding exact positional information, such as robotic surgery and advanced diagnostics. Space exploration, where parameters such as size, weight, and power consumption are critical, is set to benefit immensely from these advancements in IPGs. More efficient and reliable guidance systems for spacecraft and satellites could be a reality, facilitating deeper exploration into the unknowns of space. The exploration of new materials like 2D materials or photonic crystals, alongside groundbreaking design paradigms such as topological photonics, is paving the way for the next generation of IPGs. These new breeds of IPGs are anticipated to offer unique and enhanced functionalities, setting the stage for a future where the integration of photonic gyroscopes in everyday technology is as common as the silicon chip is today.

In sum, the future of IPGs shines bright, brimming with the potential to revolutionize diverse industries and open new chapters in scientific research. IPGs are also making inroads in several other emerging fields. In the field of wearable technology, IPGs are being explored for applications in motion tracking and health monitoring, owing to their compact size and low power consumption. They are also being tested for deployment in underwater vehicles and submarines, where accurate navigation is crucial in challenging environments with minimal GPS signal availability. In telecommunications, IPGs have the potential to be integrated into fiber optic systems to enhance stability and reduce phase noise in long-distance communication links. These emerging applications underscore the versatility and adaptability of IPGs in addressing diverse technological challenges across various sectors. The convergence of various scientific and technological domains promises not just incremental improvements but transformative changes that could redefine our interaction with technology and the world around us.

VI.   Conclusion

Here, we review advances in IPG technology and research in recent years, focusing on different types of IPGs that have been developed, including waveguide spiral-based, RLG, IPGs, and passive ring resonator IPGs, and their advantages and disadvantages. We highlight advances in improving the stability, accuracy, and resolution of IPGs, as well as the integration of IPGs with other devices to create compact, low-power navigation systems. The challenges that remain to be addressed, such as improving the long-term stability of IPGs, and possible future directions for IPG research are also discussed.